Derivadas exponenciales y logarítmicas

 

Potenciación, radicación y logaritmación

Potenciación, radicación y logaritmación son tres operaciones matemáticas

relacionadas entre sí. Potenciación: Es la operación mediante la cual una cantidad llamada base se

multiplica por sí mismo un número de veces. El resultado se llama potencia

mientras que la cantidad de veces que se multiplica la base se llama exponente. Radicación: Es una operación inversa a la potenciación, en la cual se obtiene un

número llamado raíz tal que al multiplicarlo por sí mismo el número de veces

que indica el exponente, se obtiene el radicando o subradical.

El exponente de la potencia es el índice de la raíz. Logaritmación: Es otra operación inversa de la potenciación. Consiste en hallar el

exponente al cual fue elevada la base para obtener la potencia. El resultado de la

operación se llama logaritmo y equivale al exponente de la potencia. En la logaritmación, la base puede ser cualquier número mayor que cero pero diferente

de uno. Sin embargo, normalmente sólo se utilizan dos: base 10 para los

logaritmos decimales y base e para los logaritmos naturales. El número e (número de Euler) es un número irracional. Su equivalencia

es e = 2.718281.... Un logaritmo decimal (base 10) se escribe log x mientras que un logaritmo

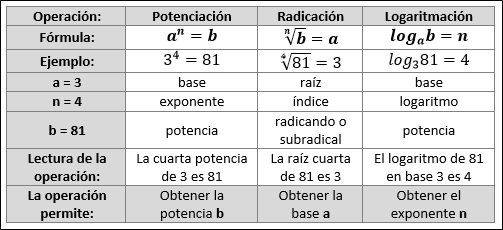
natural (base e) se escribe ln x. La tabla siguiente es una síntesis de las tres operaciones analizadas:

Función exponencial y función logarítmica Función exponencial es una función cuya ecuación es

siendo a > 0 y

La variable independiente x es el exponente. Las imágenes de f(x)

son las potencias del número a que es la base. Función logarítmica es una función cuya expresión es

, a > 0 y.

Las imágenes de f(x) son los exponentes de la potencia de base a. Las funciones exponenciales y las funciones logarítmicas son inversas entre sí, es

decir, son simétricas con respecto de la función identidad f(x) = x. En el applet que sigue se analizan gráficamente la función exponencial

f(x) = ax y la función logarítmica g(x) = logax con la base a (deslizador)

entre 0.1 y 10. De cada función se muestra su inversa. Adicionalmente se

muestran las funciones cuya base es el número de Euler: r(x) = ex y s(x) = ln x.